conjunto dos números naturais é representado pela letra maiúscula N e estes números são construídos com os algarismos: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, que também são conhecidos como algarismos indo-arábicos. No século VII, os árabes invadiram a Índia, difundindo o seu sistema numérico. Embora o zero não seja um número natural no sentido que tenha sido proveniente de objetos de contagens naturais, iremos considerá-lo como um número natural uma vez que ele tem as mesmas propriedades algébricas que os números naturais. Na verdade, o zero foi criado pelos hindus na montagem do sistema posicional de numeração para suprir a deficiência de algo nulo. Para saber mais, clique nos links: Notas históricas sobre o zero ou Notação Posicional. Caso queira se aprofundar no assunto, veja o belíssimo livro: "História Universal dos Algarismos, Tomos I e II, Editora Nova Fronteira, 1998 e 1999", de Georges Ifrah. Na sequência consideraremos que os naturais têm início com o número zero e escreveremos este conjunto como: N = { 0, 1, 2, 3, 4, 5, 6, ...}
Representaremos o conjunto dos números naturais com a letra N. As reticências (três pontos) indicam que este conjunto não tem fim. N é um conjunto com infinitos números. Excluindo o zero do conjunto dos números naturais, o conjunto será representado por: N* = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ...}
- Todo número natural dado tem um sucessor (número que vem depois do número dado), considerando também o zero.Exemplos: Seja m um número natural.
(a) O sucessor de m é m+1. (b) O sucessor de 0 é 1. (c) O sucessor de 1 é 2. (d) O sucessor de 19 é 20.
- Se um número natural é sucessor de outro, então os dois números juntos são chamados números consecutivos.Exemplos:
(a) 1 e 2 são números consecutivos. (b) 5 e 6 são números consecutivos. (c) 50 e 51 são números consecutivos.
- Vários números formam uma coleção de números naturais consecutivos se o segundo é sucessor do primeiro, o terceiro é sucessor do segundo, o quarto é sucessor do terceiro e assim sucessivamente.Exemplos:
(a) 1, 2, 3, 4, 5, 6 e 7 são consecutivos. (b) 5, 6 e 7 são consecutivos. (c) 50, 51, 52 e 53 são consecutivos.
- Todo número natural dado n, exceto o zero, tem um antecessor (número que vem antes do número dado).Exemplos: Se m é um número natural finito diferente de zero.
(a) O antecessor do número m é m-1. (b) O antecessor de 2 é 1. (c) O antecessor de 56 é 55. (d) O antecessor de 10 é 9.
Números Inteiros
A evolução dos números, assim como a dos conjuntos numéricos, ocorreu de modo a colaborar com a necessidade da humanidade. Os números inteiros apareceram quando os números naturais não satisfaziam todas as necessidades, como, por exemplo, para suprir a inexistência de números negativos no conjunto d
Os números inteiros positivos foram os primeiros números trabalhados pela humanidade e tinham como finalidade contar objetos, animais, enfim, elementos do contexto histórico no qual se encontravam.
O conjunto dos números inteiros positivos recebe o nome de conjunto dos números naturais. Sendo ele:
.jpg) ={0,1,2,3,4,5,6…}
={0,1,2,3,4,5,6…}
Enquanto que o conjunto dos números inteiros contempla também os inteiros negativos, constituindo o seguinte conjunto:
.jpg) ={…,-8,-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,7,8…}
={…,-8,-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,7,8…}
Os números inteiros estão presentes até hoje em diversas situações do cotidiano da humanidade, como, por exemplo, para medir temperaturas, contar dinheiro, marcar as horas, etc. Sua importância é indiscutível.
Diante disso, buscaremos estudar todas as propriedades desse conjunto numérico que existe há tanto tempo, perpassando pela teoria de conjuntos, intersecção de conjuntos numéricos, entre outros conceitos que fazem parte desse conteúdo.
Números racionais
Racionais Positivos e Racionais Negativos
O quociente de muitas divisões entre números naturais é um número racional absoluto.
Números racionais positivos e números racionais negativos que sejam quocientes de dois negativos que sejam quocientes de dois números inteiros, com divisor diferente de zero.
Por exemplo:
(+17) : (-4) = 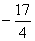
Números Racionais Positivos
Esses números são quocientes de dois números inteiros com sinais iguais.
· (+8) : (+5) 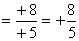
· (-3) : (-5) 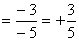
Números Racionais Negativos
São quocientes de dois números inteiros com sinais diferentes.
· (-8) : (+5) 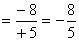
· (-3) : (+5) 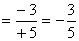
Números Racionais: Escrita Fracionária
Obs.: Todo número inteiro é um número racional, pois pode ser escrito na forma fracionária:
Denominamos número racional o quociente de dois números inteiros (divisor diiferente de zero), ou seja, todo número que pode ser colocado na forma fracionária, em que o numerador e denominador são números inteiros.
Números Irracionais
Todo número decimal é um número irracional? Para as pessoas que têm dúvida quanto a isso, veremos, neste artigo, como definir o conjunto dos números irracionais e observaremos alguns exemplos de números importantes na matemática, que são “constantes irracionais”.
Os números irracionais são aqueles que não podem ser representados por meio de uma fração. O surgimento desses números veio de um antigo problema que Pitágoras se recusava a aceitar, que era o cálculo da diagonal de um quadrado, cujo lado mede 1 unidade, diagonal esta que mede √2. Este número deu início ao estudo de um novo conjunto, representado pelos números irracionais.
.jpg)
Os números irracionais são aqueles que não podem ser representados por meio de uma fração. O surgimento desses números veio de um antigo problema que Pitágoras se recusava a aceitar, que era o cálculo da diagonal de um quadrado, cujo lado mede 1 unidade, diagonal esta que mede √2. Este número deu início ao estudo de um novo conjunto, representado pelos números irracionais.
.jpg)
Hoje em dia, pensamos: “Nossa, mas encontrar o valor de √2 é tão fácil, basta usarmos a calculadora”. Entretanto, na época em que começaram estes estudos, o único mecanismo para encontrar os valores das raízes quadradas envolvia os números quadrados (√2²,√3²,√4², …).
Com o estudo contínuo dos elementos da matemática, os matemáticos se depararam com a necessidade de calcular o comprimento de uma circunferência; e com cálculos contínuos, notaram que um número se repetia para qualquer que fosse a circunferência, número este que outrora foi denominado de número pi (π).
Com o estudo contínuo dos elementos da matemática, os matemáticos se depararam com a necessidade de calcular o comprimento de uma circunferência; e com cálculos contínuos, notaram que um número se repetia para qualquer que fosse a circunferência, número este que outrora foi denominado de número pi (π).
Esse número é encontrado através da razão do comprimento pelo diâmetro da circunferência.

Esse é um dos números que foi citado no início do texto: a constante π é de fundamental importância para a área de geometria e trigonometria.
Veremos alguns exemplos de números irracionais e notaremos que a sua parte decimal não possui nenhuma estrutura que possa ser fundamentada em forma de fração, assim como ocorre em frações periódicas.

Esse é um dos números que foi citado no início do texto: a constante π é de fundamental importância para a área de geometria e trigonometria.
Veremos alguns exemplos de números irracionais e notaremos que a sua parte decimal não possui nenhuma estrutura que possa ser fundamentada em forma de fração, assim como ocorre em frações periódicas.
Constantes irracionais ou números transcendentais:


Números irracionais obtidos pela raiz quadrada de um número:

Estes são os números irracionais, cujo valor da última casa decimal nunca saberemos.

Estes são os números irracionais, cujo valor da última casa decimal nunca saberemos.
Com isso, podemos falar que números irracionais são aqueles que em sua forma decimal são números decimais infinitos e não periódicos. Em outras palavras, são aqueles números que possuem infinitas casas decimais e em nenhuma delas obteremos um período de repetição.
O conjunto dos números irracionais é representado pela letra I ( i maiúscula)
Função de 1º grau
Definição
Chama-se função polinomial do 1º grau, ou função afim, a qualquer função f de IR em IR dada por uma lei da forma f(x) = ax + b, onde a e b são números reais dados e a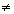 0.
0.
Na função f(x) = ax + b, o número a é chamado de coeficiente de x e o número b é chamado termo constante.
Veja alguns exemplos de funções polinomiais do 1º grau:
f(x) = 5x - 3, onde a = 5 e b = - 3
f(x) = -2x - 7, onde a = -2 e b = - 7
f(x) = 11x, onde a = 11 e b = 0
f(x) = -2x - 7, onde a = -2 e b = - 7
f(x) = 11x, onde a = 11 e b = 0
Gráfico
O gráfico de uma função polinomial do 1º grau, y = ax + b, com a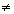 0, é uma reta oblíqua aos eixos Oxe Oy.
0, é uma reta oblíqua aos eixos Oxe Oy.
Exemplo:
Vamos construir o gráfico da função y = 3x - 1:
Como o gráfico é uma reta, basta obter dois de seus pontos e ligá-los com o auxílio de uma régua:
Como o gráfico é uma reta, basta obter dois de seus pontos e ligá-los com o auxílio de uma régua:
a) Para x = 0, temos y = 3 · 0 - 1 = -1; portanto, um ponto é (0, -1).
b) Para y = 0, temos 0 = 3x - 1; portanto,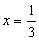 e outro ponto é
e outro ponto é 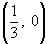 .
.
b) Para y = 0, temos 0 = 3x - 1; portanto,
Marcamos os pontos (0, -1) e 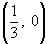 no plano cartesiano e ligamos os dois com uma reta.
no plano cartesiano e ligamos os dois com uma reta.
| 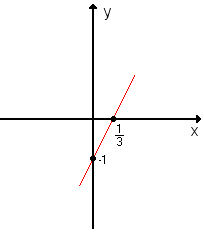 |
Já vimos que o gráfico da função afim y = ax + b é uma reta.
O coeficiente de x, a, é chamado coeficiente angular da reta e, como veremos adiante, a está ligado à inclinação da reta em relação ao eixo Ox.
O coeficiente de x, a, é chamado coeficiente angular da reta e, como veremos adiante, a está ligado à inclinação da reta em relação ao eixo Ox.
O termo constante, b, é chamado coeficiente linear da reta. Para x = 0, temos y = a · 0 + b = b. Assim, o coeficiente linear é a ordenada do ponto em que a reta corta o eixo Oy.
Zero e Equação do 1º Grau
Chama-se zero ou raiz da função polinomial do 1º grau f(x) = ax + b, a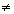 0, o número real x tal que f(x) = 0.
0, o número real x tal que f(x) = 0.
Temos:
f(x) = 0  ax + b = 0
ax + b = 0 
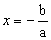
Vejamos alguns exemplos:
- Obtenção do zero da função f(x) = 2x - 5:
f(x) = 0 2x - 5 = 0
2x - 5 = 0 
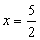
- Cálculo da raiz da função g(x) = 3x + 6:
g(x) = 0 3x + 6 = 0
3x + 6 = 0  x = -2
x = -2
- Cálculo da abscissa do ponto em que o gráfico de h(x) = -2x + 10 corta o eixo das abicissas:
O ponto em que o gráfico corta o eixo dos x é aquele em que h(x) = 0; então:
h(x) = 0 -2x + 10 = 0
-2x + 10 = 0  x = 5
x = 5
Crescimento e decrescimento
Consideremos a função do 1º grau y = 3x - 1. Vamos atribuir valores cada vez maiores a x e observar o que ocorre com y:
|
Regra geral:
a função do 1º grau f(x) = ax + b é crescente quando o coeficiente de x é positivo (a > 0);
a função do 1º grau f(x) = ax + b é decrescente quando o coeficiente de x é negativo (a < 0);
a função do 1º grau f(x) = ax + b é decrescente quando o coeficiente de x é negativo (a < 0);
Justificativa:
- para a > 0: se x1 < x2, então ax1 < ax2. Daí, ax1 + b < ax2 + b, de onde vem f(x1) < f(x2).
- para a < 0: se x1 < x2, então ax1 > ax2. Daí, ax1 + b > ax2 + b, de onde vem f(x1) > f(x2).
- SinalEstudar o sinal de uma qualquer y = f(x) é determinar os valor de x para os quais y é positivo, os valores de x para os quais y é zero e os valores de x para os quais y é negativo.
Consideremos uma função afim y = f(x) = ax + b vamos estudar seu sinal. Já vimos que essa função se anula pra raiz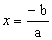 . Há dois casos possíveis:1º) a > 0 (a função é crescente)y > 0
. Há dois casos possíveis:1º) a > 0 (a função é crescente)y > 0 ax + b > 0
ax + b > 0  x >
x > 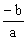 y < 0
y < 0 ax + b < 0
ax + b < 0  x <
x < 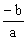 Conclusão: y é positivo para valores de x maiores que a raiz; y é negativo para valores de x menores que a raiz
Conclusão: y é positivo para valores de x maiores que a raiz; y é negativo para valores de x menores que a raiz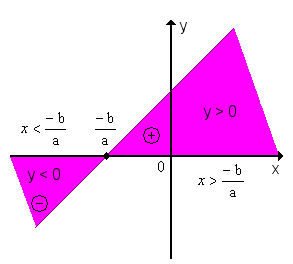 2º) a < 0 (a função é decrescente)y > 0
2º) a < 0 (a função é decrescente)y > 0 ax + b > 0
ax + b > 0  x <
x < 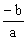 y < 0
y < 0 ax + b < 0
ax + b < 0  x >
x > 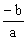 Conclusão: y é positivo para valores de x menores que a raiz; y é negativo para valores de x maiores que a raiz.
Conclusão: y é positivo para valores de x menores que a raiz; y é negativo para valores de x maiores que a raiz.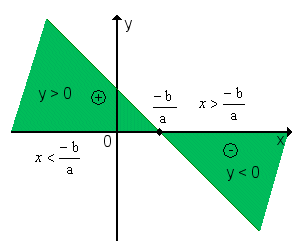
Função de 2º Grau
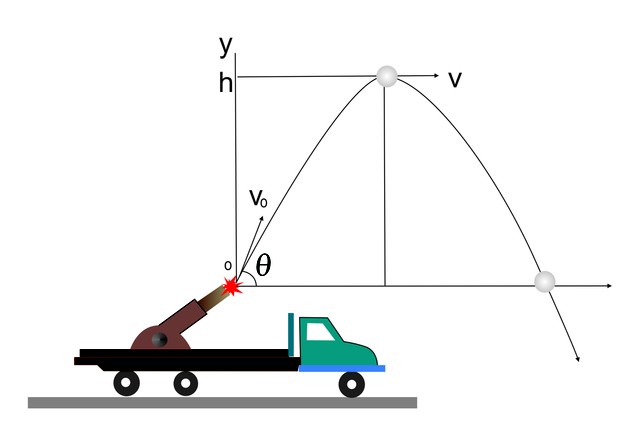
INTRODUÇÃO
DEFINIÇÃO
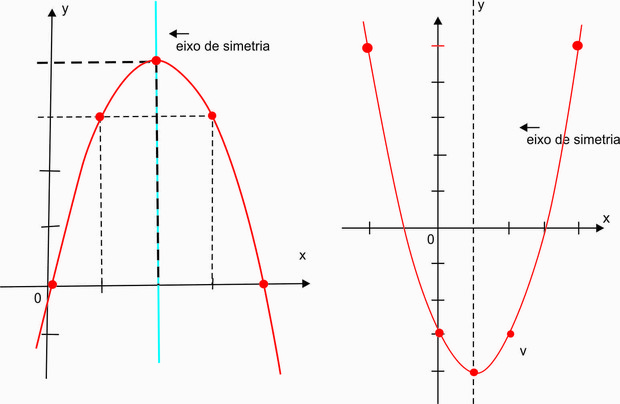
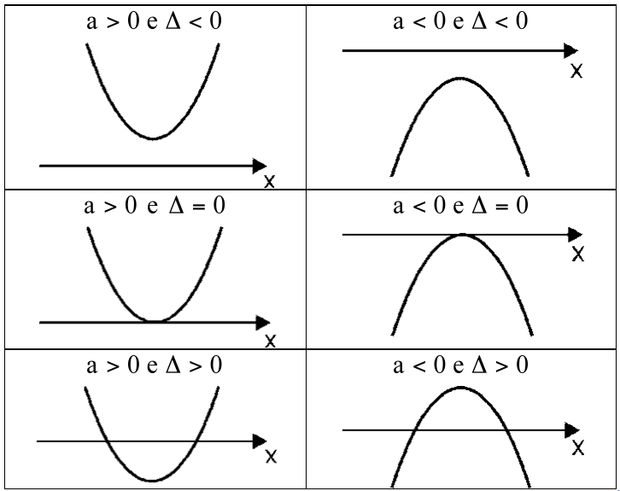
PROPRIEDADES GRÁFICAS
EXERCÍCIO
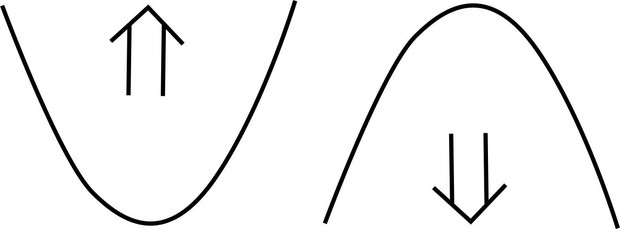
Nenhum comentário:
Postar um comentário